Origami from Divane Martínez
TRIANGULOS
lunes, 30 de mayo de 2016
lunes, 23 de mayo de 2016
Grandes Matemáticos-Pitágoras
Pitágoras
(Isla de Samos, actual Grecia, h. 572 a.C. - Metaponto, hoy desaparecida, actual Italia, h. 497 a.C.) Filósofo y matemático griego. Aunque su nombre se halla vinculado al teorema de Pitágoras y la escuela por él fundada dio un importante impulso al desarrollo de las matemáticas en la antigua Grecia, la relevancia de Pitágoras alcanza también el ámbito de la historia de las ideas: su pensamiento, teñido todavía del misticismo y del esoterismo de las antiguas religiones mistéricas y orientales, inauguró una serie de temas y motivos que, a través de Platón, dejarían una profunda impronta en la tradición occidental.Se tienen pocas noticias de la biografía de Pitágoras que puedan considerarse fidedignas, ya que su condición de fundador de una secta religiosa propició la temprana aparición de una tradición legendaria en torno a su persona. Parece seguro que fue hijo del mercader Mnesarco y que la primera parte de su vida transcurrió en la isla de Samos, que probablemente abandonó unos años antes de la ejecución del tirano Polícrates, en el 522 a.C. Es posible que viajara entonces a Mileto, para visitar luego Fenicia y Egipto; en este último país, cuna del conocimiento esotérico, Pitágoras podría haber estudiado los misterios, así como geometría y astronomía.
Algunas fuentes dicen que Pitágoras marchó después a Babilonia con Cambises II, para aprender allí los conocimientos aritméticos y musicales de los sacerdotes. Se habla también de viajes a Delos, Creta y Grecia antes de establecer, por fin, su famosa escuela en la ciudad de Crotona, una de las colonias que los griegos habían fundado dos siglos antes en la Magna Grecia (el actual sur de Italia), donde gozó de considerable popularidad y poder. La comunidad liderada por Pitágoras acabó, plausiblemente, por convertirse en una fuerza política aristocratizante que despertó la hostilidad del partido demócrata, de lo que derivó una revuelta que obligó a Pitágoras a pasar los últimos años de su vida en la también colonia griega de Metaponto, al norte de Crotona.
La comunidad pitagórica estuvo siempre rodeada de misterio; parece que los discípulos debían esperar varios años antes de ser presentados al maestro y guardar siempre estricto secreto acerca de las enseñanzas recibidas. Las mujeres podían formar parte de la hermandad; la más famosa de sus adheridas fue Teano, esposa quizá del propio Pitágoras y madre de una hija y de dos hijos del filósofo.
Más de un siglo después de la muerte de Pitágoras, en el transcurso de un viaje al sur de Italia efectuado antes de la fundación de la Academia, Platón tuvo conocimiento de la filosofía pitagórica a través de sus discípulos. Se ha afirmado que la concepción del número como principio de todas las cosas preparó el terreno para el idealismo platónico; en cualquier caso, la influencia de Pitágoras es clara al menos en la doctrina platónica del alma (inmortal y prisionera del cuerpo), que también en Platón alcanza su liberación mediante el saber.
De este modo, a través de Platón, diversas concepciones pitagóricas se convertirían en temas recurrentes o polémicos de la filosofía occidental; todavía en el siglo XVII un astrónomo tan insigne como Kepler, a quien se debe el descubrimiento de las órbitas elípticas de los planetas, seguía creyendo en la música de las esferas. Otros conceptos suyos, como los de armonía y proporción, quedarían incorporados a la música y las artes. Pitágoras ha sido visto también como el precursor de una aspiración que tendría grandísimo predicamento a partir de la revolución científica de Galieo: la formalización matemática del conocimiento.
tomado de: http://www.biografiasyvidas.com/
domingo, 22 de mayo de 2016
TEORIA Conceptos Fundamentales
DEFINICION
Un triángulo es un polígono que resulta de unir 3
puntos con líneas rectas. Se define como la porción de plano delimitada por
tres rectas que se cortan dos a dos, o como la porción común de tres semiplanos
pertenecientes a un mismo plano.
Todo triángulo tiene 3 lados (a, b y c), 3 vértices
(A, B y C) y 3 ángulos interiores (A, B y C) Habitualmente se llama lado a al
lado que no forma parte del ángulo A. Lo mismo sucede con los lados b y c y los
ángulos B y C
El triángulo es geométricamente
el polígono de menor número de lados, y a pesar de ello es el más importante,
tanto por la gran cantidad de construcciones que se pueden plantear, como por
tratarse de la figura que servirá de base para la construcción de otras más
complejas, tanto planas como espaciales.
NOMENCLATURA
DE TRIANGULOS
En la figura siguiente se
puede apreciar la nomenclatura a utilizar, para designar los diferentes
elementos de un triángulo.
Los vértices se designarán
mediante letras mayúsculas, y los ángulos correspondientes, mediante la misma
letra mayúscula o un pequeño ángulo sobre la letra. Los lados se designarán
mediante la misma letra del vértice opuesto, pero en minúscula.
El orden de las letras será el
inverso a las agujas del reloj, y cuando se trate de triángulos rectángulos, la
hipotenusa se designará con la letra “a”.
PROPIEDADES DE LOS TRIÁNGULOS:
1.
Un lado de un triángulo es menor que la suma de los otros dos y mayor que su
diferencia.
2.
La suma de los ángulos interiores de un triángulo es igual a 180°.
3.
El valor de un ángulo exterior es igual a la suma de los dos interiores no
adyacentes.
BIBLIOGRAFIA
ELEMENTOS DE UN TRIÁNGULO
En un triángulo se pueden
diferenciar los siguientes elementos:
§
Vértices: puntos en los que confluyen dos lados. Tiene 3 vértices
(A,
B
y C).
§
Lados: segmentos que unen dos vértices consecutivos del
triángulo y que delimitan su perímetro. Tiene 3 lados (a, b y c).
§ Ángulos interiores: ángulo que forman dos lados
consecutivos en el vértice en el que confluyen. Hay 3 ángulos interiores (α, β
y γ). Los ángulos interiores del triángulo suman 180º
Ángulos exteriores: ángulo de un lado con la prolongación exterior del lado consecutivo.
Hay 3 ángulos exteriores (θ). Los ángulos exteriores siempre suman 360º.
LINEAS NOTABLES DE UN TRIÁNGULO
Las principales líneas generadas en un triángulo,
reciben el nombre de alturas. La altura es cada una de las rectas
perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
Ortocentro
Es el punto de corte de las
tres alturas.
Medianas de un triángulo
Mediana es cada una de las
rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro
Es el punto de corte de las
tres medianas.
El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
BG = 2GA
Mediatrices de
un triángulo
Mediatriz es cada una de las
rectas perpendiculares trazadas a un lado por su punto medio.
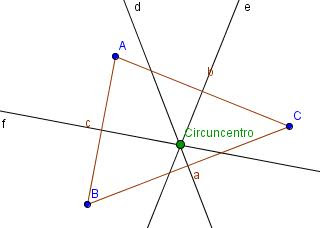
Circuncentro
Es el punto de corte de las
tres mediatrices.
Es el centro de una circunferencia circunscrita al triángulo.
Es el centro de una circunferencia circunscrita al triángulo.
Bisectrices de
un triángulo
Bisectriz es cada una de las
rectas que divide a un ángulo en dos ángulos iguales.
Incentro
Es el punto de corte de las
tres bisetrices. Es el centro de una circunferencia inscrita en el triángulo.
Recta de Euler
El ortocentro, el baricentro y
el circuncentro de un triángulo no equilátero están alineados; es decir,
pertenecen a la misma recta, llamada recta de Euler.
BIBLIOGRAFIA
CLASIFICACIÓN
DE LOS TRIÁNGULOS:
Los triángulos podemos clasificarlos según 2
criterios:
Según la medida de sus lados
- Equilátero
Los 3 lados
son iguales
Los 3 ángulos interiores son iguales
- Isósceles
Tienen 2 lados iguales y un lado distinto (c)
Los ángulos
A y B son iguales, y el otro agudo es distinto
- Escaleno
Los 3 lados son distintos
Los 3 ángulos son también distintos
Según la medida de sus ángulos
-
Acutángulo
Tienen los 3 ángulos agudos (menos de 90 grados)
-
Rectángulo
El ángulo interior A es recto (90 grados) y los
otros 2 ángulos son agudos
Los lados que forman el ángulo recto se llaman
catetos (c y b), el otro lado hipotenusa
-
Obtusángulo
El ángulo interior A es obtuso (más de 90 grados)
Los otros 2 ángulos son agudos
BIBLIOGRAFIA
http://www.dibujotecnico.com/definicion-nomenclatura-clasificacion-y-propiedades-de-los-triangulos/
CONGRUENCIA DE TRIÁNGULOS
Dos
triángulos son congruentes si tienen sus lados y ángulos correspondientes
congruentes. Para saber si dos triángulos son congruentes no es necesario
verificar unos criterios de congruencia:
Criterio
Lado-Lado-Lado (LLL) en
el cual se pide verificar que si los tres pares de lados son congruentes
dos a dos, entonces los tres ángulos correspondientes serán congruentes.
Criterio
Lado- Ángulo-Lado(LAL) mediante
el cual basta verificar que dos pares de lados de los triángulos sean
congruentes así como el ángulo comprendido entre ellos.
Criterio
Ángulo-Lado-Ángulo(ALA) en este
criterio se verifica únicamente que dos ángulos correspondientes sean
congruentes, así como el lado común a los dos ángulos.
Cuando el triángulo es
rectángulo los criterios son menos exigentes pues ya se sabe que uno de los
ángulos es de 90º.
RAZON DE SEMEJANZA DE TRIANGULOS
Se llaman figuras semejantes aquellas que tienen
igual forma, pero diferente tamaño. Bajo este contexto, se denomina razón de semejanza en un triángulo al
cociente entre dos longitudes correspondientes. r = a' / a
La semejanza de triángulos es una de las herramientas más fuertes de la
geometría, mediante la cual se resuelven numerosos problemas de aplicación. Ser
semejante significa tener la misma forma, en el caso de los triángulos ser
semejante, entonces, está referido a tener los ángulos correspondientes
congruentes.
Dos triángulos son
semejantes si tienen los ángulos iguales, y sus lados homólogos proporcionales.
Los casos de semejanza de
los triángulos ofrecen tres posibilidades,
1. Dos triángulos son
semejantes cuando tienen dos ángulos respectivamente iguales
2. Dos triángulos son
semejantes cuando tienen un ángulo igual comprendido por lados proporcionales.
3. Dos triángulos son
semejantes cuando tienen sus catetos (lados) proporcionales
CASOS DE SEMEJANZAS DE DOS TRIÁNGULOS RECTÁNGULOS.
ü Dos
triángulos rectángulos son semejantes si tienen un ángulo agudo igual.
ü Dos
triángulos rectángulos son semejantes si tienen los dos catetos
proporcionales.
ü
Dos triángulos rectángulos son semejantes si tienen
proporcionales la hipotenusa y un cateto.
La conclusión más trascendental
de este hecho es que cuando dos triángulos son semejantes los lados
correspondientes son proporcionales, es decir, que las razones entre lados
correspondientes de los dos triángulos son iguales.
BIBLIOGRAFIA
TEOREMAS EN LOS TRIÁNGULOS
Teorema de Pitágoras
Este teorema, enunciado por el matemático griego Pitágoras en el
siglo V a.C., es uno de los resultados más conocidos e importantes de la geometría
y posee gran cantidad de aplicaciones tanto en distintas partes de las
matemáticas como en situaciones de la vida diaria.
El teorema se aplica a los triángulos rectángulos, y dice lo
siguiente:
"En un triángulo
rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de
los catetos"
Si llamamos "a" a la hipotenusa de un triángulo
rectángulo y "b", "c" a los catetos, se verifica: a2 =b2+c2
A los grupos de tres números "a", "b" y
"c" que verifican a2=b2+c2 se les
llama "ternas pitagóricas".
Gráficamente, el teorema de Pitágoras se expresa de la forma
siguiente:
Teorema de la Altura
Sea un triángulo rectángulo, cuyos catetos denotaremos por
"b" y "c", siendo "a" la hipotenusa (lado opuesto
al ángulo recto) y "h" la altura del triángulo sobre la hipotenusa:
De las tres alturas que tiene un triángulo rectángulo, dos de
ellas son los catetos; y la tercera, la altura sobre la hipotenusa, está
relacionada con los lados del triángulo por la siguiente relación:
"El producto de
los dos catetos, de un triángulo rectángulo, coincide con el producto de la
hipotenusa por la altura sobre ella"
h2 =
m⋅n
El resultado anterior se conoce con el nombre de Teorema de la
Altura, y se enuncia de la siguiente manera:
"En un triángulo
rectángulo, el cuadrado de la altura sobre la hipotenusa es igual al producto
de las proyecciones de los catetos sobre la hipotenusa”
Teorema del Cateto
Se conocen con el nombre de Teorema del cateto que se enuncia de
la siguiente forma:
"El cuadrado de
un cateto es igual al producto de la hipotenusa por la proyección del cateto
sobre la hipotenusa"
BIBLIOGRAFIA
ENLACES SUGERIDOS
ENLACES
REPOSITORIO DEL SENA SOBRE TRIANGULOS
WEB QUEST DE ANDALUCIA
ACTIVIDADES DE FLAGSTAFF, REPOSITORIO DE EJERCICIOS
WIKIS ESPAÑOLAS
APLICACION EN AULA 365 ARGENTINA
EDITORIAL ESPAÑOLA RECOMIENDA
ACTIVIDAD DIDACTICA SOBRE EL TEOREMA DE PITAGORAS
EJERCICIOS DE APLICACION TEOREMA DE PITAGORAS
GRANDES MATEMATICOS
GRANDES MATEMATICOS
Principales Aportes de Pitagoras
En
matemáticas la demostración del famoso teorema de la relación de los
lados del triángulo rectángulo. Halló en música las relaciones entre
números enteros que producían acordes agradables al oído. Fue uno de los
primeros en defender la forma esférica para la Tierra, y el que se dio
cuenta por primera vez que la estrella matutina y la vespertina eran
una misma, el planeta Venus.
Creó una escuela filosófica con gran dedicación a la matemática
Creó una escuela filosófica con gran dedicación a la matemática
Entre
las amplias investigaciones matemáticas realizadas por los pitagóricos
se encuentran sus estudios de los números pares e impares y de los
números primos y de los cuadrados, esenciales en la teoría de los
números. En geometría el gran descubrimiento de la escuela fue el
teorema de la hipotenusa, conocido como teorema de Pitágoras, que
establece que el cuadrado de la hipotenusa de un triángulo rectángulo es
igual a la suma de los cuadrados de los otros dos lados.
Teorema: el cuadrado de la hipotenusa de un triangulo rectangular es la suma de los cuadrados de sus catetos (este teorema ya había sido descubierto por los Babilonios y quizás también los hindúes pero seguramente Pitágoras lo descubrió de forma independiente)
- Fundó la primera escuela para cultiva el conocimiento, las artes, una vida de sabiduría.
- Fue el primero en usar las palabras para explicar cuestiones matemáticas.
- Lo mismo se puede decir sobre las palabras y la filosofía del cosmos (=orden del universo, basado en relaciones numéricas y leyes universales). Quizás también la palabra música el la utilizó con el sentido en que nosotros la utilizamos hoy.
- La representación de los cuerpos geométricos regulares.
- Contribuciones a la aritmética básica y la teoría general de los números.
- La distinción entre números y pares e impares
- Establecimiento de una escala cuantitativa de notas musicales
IMPORTANCIA
- Cualitativa. Avance en geometría.
- La racionalidad alcanzó un altísimo nivel de abstracción y cuantificación.
- Diseño de un orden en los objetos abstractos para su posterior sistematización.
- Focalización y desarrollo de una concepción metafísica de la realidad.
tomado de: http://oscarly-mantenimientopc.blogspot.com.co
Suscribirse a:
Comentarios (Atom)





























 tomado de:
tomado de: